Use the Shells Method to set up (do not evaluate) an integral for the volume of the solid...
Question:
Use the Shells Method to set up (do not evaluate) an integral for the volume of the solid obtained by rotating the region enclosed by {eq}y = 4x - x^2 {/eq} and y = 0 about the y-axis.
Volume of Solid of Revolution:
Since using the cylindrical shell method thus the formula to use is {eq}V=2\pi \int_{a}^{b}rh\:dr {/eq} where {eq}r {/eq} is the centroid of the region, {eq}h {/eq} is the height and {eq}dr {/eq} is the width. The limits of integration are the intersections between the given equations.
Answer and Explanation: 1
Become a Study.com member to unlock this answer! Create your account
View this answerBelow is the graph,
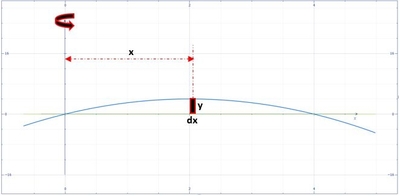 |
From the graph,
{eq}r=x,\:h=y,\:dr=dx {/eq}
Substituting to the formula {eq}V=2\pi \int_{a}^{b}rh\:dr {/eq}
Thus,...
See full answer below.
Ask a question
Our experts can answer your tough homework and study questions.
Ask a question Ask a questionSearch Answers
Learn more about this topic:

from
Chapter 14 / Lesson 5The volume of a revolution can be calculated using the slicing method, the disk method, and the washer method. Explore the processes of the three methods and discover how to use them to find the volumes of revolution.
Related to this Question
- Use the Shells Method to set up (do not evaluate) an integral for the volume of the solid obtained by rotating the region enclosed by the curve y = 4x - x^2 and y = 0 about the y-axis.
- Using the method of shells, set up, but don't evaluate the integral, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis: \ y=
- Using Shells method, set up the integral that gives the volume of the solid obtained by rotating the region bounded by y = 2x, \; y = 4, \; x = 0 about the y-axis.
- The volume of the solid obtained by rotating the region enclosed by y = 6x - 2x^2, y = 0 about the y-axis can be computed using the method of cylindrical shells via an integral. Set up the integral th
- The volume of the solid obtained by rotating the region enclosed by y=56x-8x^2, y=0 about the y-axis can be computed using the method of cylindrical shells via an integral.
- Compute the volume, using the method of cylindrical shells via an integral, of the solid obtained by rotating the region enclosed by y=48x-6x^2, y=0 about the y-axis.
- Use the Shell Method to compute the volume of the solid obtained by rotating the region enclosed by the curves y = x^2 and y = 8 - x^2 about the y-axis.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. a) y = 14x^2, y = 0, x = 4 b) y = x^2, y = 4x, x = 2
- Compute the volume of the solid obtained by rotating the region enclosed by y = 1/(x^5), y = 0, x = 2, x = 7 about the y-axis using the method of cylindrical shells.
- The volume of the solid obtained by rotating the region enclosed by y=1/x^5, y=0, x=2, x=4 can be computed using the method of cylindrical shells via an integral
- Use the shell method to determine the volume of the solid obtained by rotating the region bounded by the given curves about the indicated axis. a) y = \frac{1}{x}, x = 1, x = 2, y = 0; about y-axis. b
- Let V be the volume of the solid S obtained by rotating about the y-axis the region bounded by y = \sqrt{4x} and y = 2x^2. Find V both by slicing and by cylindical shells: A. The method of cylindrica
- Use shells to compute the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. x = 1 + (y-2)^2, x = 2; about the x-axis
- Use the Shell Method to compute the volume of the solid obtained by rotating the region enclosed by the graphs y = x^2 \enspace and \enspace y = \sqrt x about the y-axis.
- Use the Shell Method to compute the volume of the solid obtained by rotating the region enclosed by the graphs as indicated, about the y-axis. f(x) = 3x - 2, g(x) = 6 - x, x = 0.
- Use the Shell Method to compute the volume, V, of the solid obtained by rotating the region enclosed by the graphs as indicated, about the y-axis. y = x^2, y = x^(1/2).
- Set up (but do not evaluate) the integral that gives the volume of the solid obtained by rotating the region bounded by y = 2 x ? x 2 and the x -axis about (a) the x -axis using the method of dis
- Use the method of cylindrical shells to and the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. y=\sqrt{(x)}; x=0; y=2
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bound by x=28y^2 - 7y^3, x=0 about the x-axis.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the region bounded by y = 1/x, the x-axis, x = 3, and x = 4, about the x-axis.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = 6x, y = 18, x = 0.
- Use the shell method to set up and evaluate an integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = 14x - x^2, x = 0, y = 49
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the x-axis. y = sqrt{x + 20} y = x y = 0
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. x = 4, y = x^3, y = 0.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = 4x - x^2, x = 0, y = 4.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the x-axis. y = x^2, x = 0, y = 16.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = 8x - x^2 x = 0 y = 16
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = 6 x, y = 18, x = 0.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = x^3, y = 0, x = 4.
- Let R be the region bounded by y = 4 - x^2 and the x-axis where 0 < x < 2. Use the method of cylindrical shells to find the volume of the solid obtained by rotating R about the y-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by x= \sqrt y, x=0 ,y =7 about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y = \sqrt{x - 4}, y = x-4 about the y - axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y = 3+ 2x-x^2, x+y = 3 about the y-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by x = sqrt(y), x = 0, and y = 2, about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y=8x^{(\frac{1}{2})} \ and \ y=8x^2 about the __y__ axis
- The volume of the solid obtained by rotating the region enclosed by y = x^2, \\ x = 2, \\ x = 5, \\ y = 0 about the line x = 7 can be computed using the method of cylindrical shells via an integral. F
- Use the Shell Method to set up the integral that will give the volume obtained by rotating the region enclosed by the graphs of y = \sqrt x and y = x^2 about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bound by the curves xy = 9 , x=0,y=9, y=11 about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves x = 1 + (y - 7)^2, x = 17 about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves x = 16\sqrt y , x = 0, y=1 about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. xy = 9, x = 0, y = 9, y = 11.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x + y = 4, \quad x = {y^2} - 4y + 4
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves y = x^2 , \ y = 4x - x^2 and the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. xy = 5, x = 0, y = 5, y = 7
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. xy = 3 x = 0 y = 3 y = 5
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves y=4x-x^2 and y=x about the y axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by curves y = x^2, and y = 6x - x^2 and the y-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves y = 4x^2 and 2x + y = 6 about the x-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. xy = 2, x = 0, y = 2, y = 4
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating about the y-axis the region bounded by y = 3 + 2x - x^2, x + y = 3.
- Use the Shell Method to compute the volume, V, of the solid obtained by rotating the region enclosed by the graphs of y = x^4 \enspace and \enspace y = x^{1/4} about the y-axis.
- Use the Shell Method to compute the volume,of the solid obtained by rotating the region enclosed by the graphs y = x^4 \enspace and \enspace y = x^{1/4} about the y-axis.
- The volume of the solid obtained by rotating the region bounded by y = x^2, y = 5 x about the line x =5 , can be computed using the cylindrical shell method via the integral V = .
- 1. Use the shell method to set up and evaluate an integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = 25 -x^2, y = 0 2. Use the shell method to
- 1. Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x = 1 + (y - 5)^2, x = 17 2. Use the method of cy
- 1) Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. y = x^{3/2}, y = 8, x = 0 2) Use the method of cy
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. y = \sqrt x, \enspace x = 0, \enspace y = 2
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. xy=1, x=0, y=1, y=3.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. y=x^3, y=8, x=0
- Consider the solid obtained by rotating the region between the curves x=y^{2}+2 \quad y=x-2 about the x-axis. a.Using the method of shells, set up an integral for the volume of the solid. Do not eva
- Use the method of cylindrical shells to compute the volume V of the solid obtained by rotating the region bounded by the given curves about the x-axis: x = 4 + y^2, x = 0, y = 1, y = 3.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y = x^2, y = 4x - x^2.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. y=4-x^2, y=0.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region y = 3 - x about the y-axis.
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bound by the curves y = x^2 \enspace and \enspace y = 8x-x^2 about the x-axis.
- Set up an integral to compute the volume of the solid obtained by rotating the region enclosed by y = x^2, x = 1, x = 3, y = 0 about the line x = 5 using the method of cylindrical shells.
- Set up an integral to compute the volume of the solid obtained by rotating the region enclosed by y = 1/x^4, y = 0, x = 3, x = 5 about the line x = -2 using the method of cylindrical shells.
- Using the shell method. Find the Volume of the solid obtained by rotating the region bounded by the given curves y = 8x^2, x = 1, y = 0 about the x-axis.
- Use the shell method to find the volume of the solid obtained by rotating the region bounded by the curves y = 2x^2 - x^3, about the y-axis.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region bounded by y = \frac{1}{x}, x=7,x=8 about the x-axis.
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region bounded by y = x^2, x = 0, y = 16 about the x-axis.
- Use the Shell method to find the volume of the solid obtained by rotating the region bounded by x=3y-y^2 and the y-axis about the x-axis.
- 1.) Use the method of cylindrical shells to find the volume V of the solid obtained by rotating the region bounded by the given curves about the x-axis. y = x^3, y = 27, x = 0 2.) Set up the integral
- Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y = square root{x}, x = 0, and y = 2 about the x - axis
- Use the Shell method to find the volume of the solid obtained by rotating the region bounded by y = 3\sqrt x, x=0, x=4 about the y-axis.
- Use the shell method to find the volume of the solid obtained by rotating the region bounded by y = x - x^2, y =0 about the y-axis.
- Use the shell method to find the volume of the solid obtained by rotating the region bounded by y = x^2, y = 3+ 2x ; \quad x \geq 0 about the y-axis.
- Use the Shell method to find the volume of the solid obtained by rotating the region bounded by y = 3\sqrt x, x=0, y = 0 about the y-axis.
- Use the shell method to find the volume of the solid obtained by rotating the region bounded by \displaystyle y=\sqrt{x^2+1}, \ \ \ y=0 \ \ and 0\leq x \leq \sqrt{3} about the y-axis.
- Use the method of cylindrical shells to find the volume \displaystyle V of the solid obtained by rotating the region bounded by the given curves about the \displaystyle x-axis. \displaystyle x=4+(y-7)
- The volume of the solid obtained by rotating the region bounded by y = e^x, y = ln x, x = 1, and x = 4 about the line y-axis can be computed using the method of cylindrical shells. Using the method of cylindrical shells, set up the integral. Find volume.
- Use the method of cylindrical shells to set up an integral which gives the volume of the solid generated by rotating the region bounded by x + y = 3 and x = 4 - (y - 1)^2 about the x-axis.
- Use the Shell Method to set up the and evaluate the integral that gives the volume of the solid obtained by revolving the region bounded by y = \sqrt x , y = 0, and x = 4 about the y-axis.
- Let V be the volume of the solid S obtained by rotating about the y-axis the region bounded by y = sqrt(4x) and y = 2x^2. Find V both by slicing and by cylindrical shells: A) The method of slicing. B)
- Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the region bounded by y = x^2, x = 0, y = 16 about the x-axis.
- Calculate the volume of the solid obtained by rotating the region bounded by the given curves about the indicated axis. Use the cylindrical shells method. y = 2x^2, y = x^2 + 1, x = 0, about x = 2
- Using the Method of Cylindrical Shells, the integral to find the volume of the solid obtained by revolving the region bounded by the curves y= 1 / x^2+1 and y = 0, x = 0, and x = 6 about the y-axis.
- Use the method of cylinders (shell method) to determine the volume of the solid obtained by rotating the region bounded by the given curves about the given axis. Rotate the region bounded by y = \frac{1}{x}, x = \frac{1}{2}, x = 4 and the x-axis about the
- Use the method of cylindrical shells to find the volume of the solid generated by rotating the region bounded by the curves about the given axis. y = e^x, x = 0, y = 3; about the x-axis.
- Use the cylindrical shell method to find the volume of the solid obtained by rotating the region bounded by the curves y = 4x - x^2 and y = x about the y-axis.
- The volume of the solid obtained by rotating the region bounded by y = ex, y = ln x, x = 1, and x = 5 about the line y-axis can be computed using the method of cylindrical shells. Find the volume of the solid using the method of cylindrical shells.
- cFind the volume of the solid obtained by rotating the region enclosed by y = 12x-3x^2,y=0 about the y-axis using the method of cylindrical shells.
- Compute the volume of the solid obtained by rotating the region enclosed by x = 6 y and y 3 = x (with y ? 0 ) about the y-axis using the method of disks or washers via an integral.
- Use the method of cylindrical shells to set up (do not evaluate) the integral of the volume of the solid obtained by revolving the region y=sin x, y=0, x=0 about the line x = 4
- Use the Shell Method to compute the volume V, of the solid obtained by rotating the region enclosed by the graphs as indicated, about the y-axis. y=x^4 and y=x^{\frac{1}{4.
- 1.Let R denote the region bounded by the curves y = x, x = 0 and y = 2. Use the method of cylindrical shells to find the volume of the solid obtained by rotating R about the x-axis. 2. Let R be the r
- Use the shell method to find the given volume of rotation. The solid obtained by rotating the region bounded by y = square root{sin^{-1} x}, the x-axis, and x = 1 about the x-axis.
- Use the shell method to set up and evaluate the volume of the solid generated by revolving the plane region bounded by y = \sqrt {x + 20}, y = x, y = 0 about the x-axis.
- Use the method of cylinder shells to find the volume of the solid obtained by rotating the region bounded by the given curve about the x-axis. y=x^{2/3}, y=8, x=0.