Find the area of {eq}r^2 = \sin{2 \theta } {/eq} for {eq}0 \leq \theta \leq \pi/2 {/eq}.
Question:
Find the area of {eq}r^2 = \sin{2 \theta } {/eq} for {eq}0 \leq \theta \leq \pi/2 {/eq}.
Area in Polar Coordinates:
The formula in finding the area of the region under polar curve is {eq}A=\int_{a}^{b}\frac{1}{2}r^{2}d\theta {/eq} where {eq}r {/eq} is the radius and {eq}d\theta {/eq} is the differential angle.
Here, the given limits is {eq}0 \leq \theta \leq \pi/2 {/eq}
Answer and Explanation: 1
Become a Study.com member to unlock this answer! Create your account
View this answerBelow is the graph,
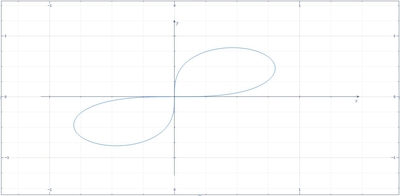 |
Using the formula the area of the region is,
{eq}A=\int_{0}^{\frac{\pi }{2}}\frac{1}{2}\left ( \sqrt{\sin 2\theta }...
See full answer below.
Learn more about this topic:
from
Chapter 24 / Lesson 1Learn how to graph polar equations and plot polar coordinates. See examples of graphing polar equations. Transform polar to rectangular coordinates and vice versa.
