A wooden beam has a rectangular crosssection of height h in. and width w in. (see the...
Question:
A wooden beam has a rectangular cross-section of height {eq}h\text{ in.} {/eq} and width {eq}w\text{ in.} {/eq} (see the accompanying figure). The strength {eq}S {/eq} of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross-section of the strongest beam that can be cut from a round log of diameter {eq}d=25\text{ in.} {/eq}?
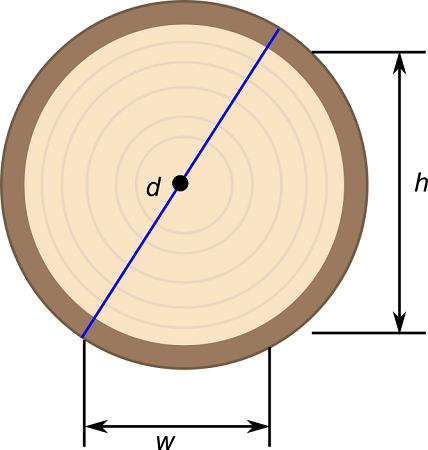 |
Maximum & Minimum:
To find the quantity that is maximum on some value of a variable, we need first to develop a relationship between the variable and that quantity. Then we will use the differentiation technique to get the maximum point.
Answer and Explanation: 1
Become a Study.com member to unlock this answer! Create your account
View this answer
The diameter is given as:
{eq}d^2=w^2+h^2 {/eq}
Now, the strength is given as:
{eq}S= w+h^2\\ \Rightarrow S= w+(d^2-w^2)~~~~~~~~~\left [...
See full answer below.
Ask a question
Our experts can answer your tough homework and study questions.
Ask a question Ask a questionSearch Answers
Learn more about this topic:

from
Chapter 9 / Lesson 3Learn to define the maximum and minimum values of a graph. Know how to find local and absolute maximum and minimum values on a graph with examples.
Related to this Question
- A wooden beam has a rectangular cross section of height H and width W. The strength S of the beam is directly proportional to the width and the square of the height. Find the dimensions of the stronge
- A wooden beam has a rectangular cross section of height h and width w. The strength S of the beam is directly proportional to the width and the square of the height. What are the dimensions of the s
- A wooden beam has a rectangular cross-section of height h in. and width w in. (see the accompanying figure). The strength S of the beam is directly proportional to its width and the square of its heig
- A wooden beam has a rectangular cross section of height h and width w. The strength S of the beam is directly proportional to the width and the square of the height. What are the dimensions of the str
- A wooden beam had a rectangular cross-section of height (h) in. and width (w) in. The strength (S) of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross-section of the strongest beam that can
- A wooden beam has a rectangular cross-section of height h in. and width w in. The strength S of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross-section of the strongest beam that can be cut
- The strength S of a rectangular wooden beam is proportional to its width times the square of its depth. Find the dimensions of the strongest beam that can be cut from a 10-in.-diameter cylindrical log
- The strength of a rectangular beam of a given length is proportional to the width times the square of the height of a cross-section, that is,\\ S = w \cdot h^2 \\ where S is the strength (in some app
- The strength of a rectangular beam is proportional to the product of its width w and the square of its depth h. Find the dimensions of the strongest beam that can be cut from a wooden log of diameter
- The strength of a beam with rectangular corss-section is directly proportional to the product of the width and the square of the depth (thickness from the top to bottom of the beam). Find the shape of
- The strength of a beam with rectangular cross-section is directly proportional to the product of the width and the square of the depth (thickness from the top to bottom of the beam). Find the shape of
- A rectangular beam will be cut from a cylindrical log of radius r = 40 inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth.
- A rectangular beam is cut from a cylindrical log of radius 25 cm. The strength S of a beam of width w and height h is proportional to wh^2. Find the width and height of the beam of maximum strength.
- A rectangular beam is cut from a cylindrical log of radius 48 cm. The strength of a beam of width w and height h is proportional to wh^2. Find the width and height of the beam of maximum strength.
- A rectangular beam is cut from a cylindrical log of radius 30 cm. The strength of a beam of width w and height h is proportional to wh^2. Find the width and height of the beam of maximum strength. Is
- A rectangular beam will be cut from a cylindrical log of radius 10 \sqrt 3 inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its de
- The strength of a rectangular beam cut from a particular type of wooden log is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from a wooden log of diameter 18 inches for this
- A rectangular beam is cut from a cylindrical log of radius 25 cm. The strength of a beam of width w and height h is proportional to wh^2. Find the width and height of the beam of max
- If the strength of a rectangular beam of wood varies as its breadth and the square of its depth, find the dimensions of the strongest beam that can be cut out of a round log, diameter d.
- The strength, S, of a beam with a rectangular cross section is directly proportional to the product of its width, w, and the square of its depth, d. Find the dimensions of the strongest beam that can
- A rectangular beam is cut from a cylindrical log of radius 30 cm. The strength of a beam of width w and height h is proportional to { wh^2 }. Find the width and height of the beam of maximum strengt
- The strength of a rectangular beam varies jointly as its width and the square of its depth. If the strength of a beam 4 inches wide by 12 inches deep is 1800 pounds per square inch, what is the strength of a beam 5 inches wide and 12 inches deep?
- The strength of a rectangular beam varies jointly as its width and the square of its depth. If the strength of a beam 10 inches wide by 20 inches deep is 3400 pounds per square inch, what is the strength of a beam 9 inches wide and 18 inches deep?
- The strength of a wooden beam is proportional to the product of its width and the square of its height as shown below. What are the dimensions of the strongest beam that can cut from a log with diameter 12 inches.
- The strength of a wooden beam is proportional to the product of its width and the square of its height. What are the dimensions of the strongest beam that can be cut from a log with diameter 12 inche
- The stiffness of a rectangular beam for a particular type of wood is proportional to the product of its width w and the cube of its depth h. Find the dimensions of the stiffest beam that can be cut from a wooden log of diameter 15 inches? What is the opti
- Find: The strength of a rectangular wooden beam is proportional to its width times the cube of its thickness (that is,thickness ^3 ).Find the dimensions of the strongest rectangular beam that can be c
- The strength of a rectangular beam is proportional to width*depth^2. What are the dimensions of the strongest rectangular beam that can be cut out of a 12 inch diameter log?
- a rectangular box of length l and width w rests against a wall, making an angle \u03b8 with respect to the floor. what is the height h of the top edge of the box above the floor?
- A rectangular beam is cut from a cylindrical log of radius 33cm. The strength of a beam of width \omega and height h is proportional to \omega h^2. (See the figure below.) Find the width and height o
- 1. Of all rectangles with given area, A, which has the shortest diagonals? 2. A rectangular beam is cut from a cylindrical log of radius 30 cm. The strength of a beam of width w and height h is propo
- The safe load, L, of a wooden beam supported at both ends varies jointly as the width, w, and the square of the depth, d, and inversely as the length, l. A wooden beam 2 in. wide, 6 in. deep, and 8 ft long holds up 24090 lb. What load would a beam 9 in. w
- A rectangular box which is open at the top can be made from a 12-by-30-inch piece of metal by cutting a square from each corner and bending up the sides. Find the dimensions of the box with greatest volume, where h = height, l = length, and w = width. (No
- The strength of a beam with a rectangular cross section varies directly with x and with the square of y. What are the dimensions of the strongest beam that can be sawed out of a round log with diamet
- A rectangular beam will be cut from a cylindrical log of radius 10 inches. (a) Show that the beam of maximal cross-sectional area is a square. (b) Four rectangular planks will be cut from the four sections of the log that remain after cutting the square
- A rectangular box which is open at the top can be made from an 24-by-30-inch piece of metal by cutting a square from each corner and bending up the sides. Find the dimensions of the box with greatest volume. (Note: let the width be determined by the 24-in
- The sag (in inches) in a beam of wood of length L (in inches), width w (in inches), and height h (in inches), is given by S=.0004\frac{L^4}{wh^3}. A beam measures 36 inches long, 2 inches wide, and 6
- Suppose that the maximum weight that a certain type of rectangular beam can support varies inversely as its length and jointly as its width and the square of its height. Suppose also that a beam 6 inc
- Suppose that the maximum weight that a certain type of rectangular beam can support varies inversely as its length and jointly as its width and the square of its height. Suppose also that a beam 3 inches wide, 4 inches high, and 6 feet long can support a
- The area of 20 square ft of a wooden board may be used to build a box. The base of the box must be a rectangle whose ratio of the sides is 2: 3. What are the dimensions of the box that maximize its vo
- The width and the length of a rectangular piece of plywood are 4 feet and 8 feet, respectively. Along one edge of the plywood, a strip x inches wide and 8 feet long is removed. Then, along an edge perpendicular to the 8-foot edge
- A box (with no top) is to be constructed from a piece of cardboard of sides A and B by cutting out squares of length h from the corners and folding up the sides. Which value of h maximizes the volume if A = B?
- A box (with no top) is to be constructed from a piece of cardboard of sides A and B by cutting out squares of length h from the corners and folding up the sides. Suppose that the box height is h = 1 i
- The width and the length of a rectangular piece of plywood are 4 feet and 8 feet, respectively. Along one edge of the plywood, a strip x inches wide and 8 feet long is removed. Then, along an edge perpendicular to the 8-foot edge, a strip x inches wide is
- The width of a rectangular gate is 2 meters (m) larger than its height. The diagonal brace measures square root of 6. Find the width and height.
- A carpenter has to cut a rectangular beam from a circular log. The strongest rectangular beam is the one whose length is 2.3 times the radius of the log. What is the length of the strongest beam that can be cut from a log 12 inches in diameter? Justify.
- A rectangular prism of volume 3200 mm^3 has a rectangular base of length 10 mm and width 8 mm. Find the height h of the prism.
- An open box with a rectangular base is to be constructed from a rectangular piece of cardboard, 16 inches wide and 21 inches long, by cutting out a square from each corner and then bending up the side
- A rectangular plate 12ft long and 8 ft wide is submerged vertically with the longer edge in the surface of the water. Find the force on one side of the plate.
- An open box with a rectangular base is to be constructed from a rectangular piece of cardboard 16 inches wide and 21 inches long by cutting out a square from each corner and then bending up the resulting sides. Find the size of the corner square that will
- An open box with a rectangular base is to be constructed from a rectangular piece of cardboard 16 inches wide and 21 inches long by cutting out a square from each corner and then bending up the sides.
- A trough is to be made of a long rectangular piece of tin by bending up the two long edges so as to give a rectangular cross section. If the width of the piece is 25 inches, how deep should the trou
- Consider a window the shape of which is a rectangle of height h h surmounted by a triangle having a height h that is 1.5 times the width w of the rectangle. If the cross-sectional area is A, determine
- A rectangular box is to be made out of 1200 cm2 of paper material. The box is to have no top. The base of the box is to be a square. The height can be anything. Find the length, width and height of th
- An open box with a rectangle base is to be constructed from a rectangular piece of cardboard 16 inches wide and 21 inches long by cutting a square from each corner and then bending up the resultant side. Find the size of the corner square that will produc
- A 3 foot wide deck will be built around a rectangular shaped pool that measures 15 feet by 30 feet. The resulting shape is also rectangular. If the lumber $10 per square yard, what is the cost of the wood for the deck?
- Consider a window the shape of which is a rectangle of height hh surmounted by a triangle having a height T that is 1.5 times the width ww of the rectangle (as shown in the figure below). If the cross
- The rectangular top of a table is three times as long as it is wide. Its width is 30 centimeters. Find the area of the table top.
- A rectangular box is made from a piece of cardboard 31 cm by 17 cm by cutting equal squares from each corner and bending up the sides. Express the volume of the box as a function of the side of the sq
- An open top box with a rectangular base is to be constructed from a rectangular piece of cardboard 16 inches wide and 21 inches long by cutting a square from each corner and then bending up the resulting sides. Find the size of the corner square that will
- A 3-foot-wide wood deck will be built around a rectangular-shaped pool that measures 15 feet by 30 feet. The resulting shape is also rectangular. If the lumber costs $10 per square yard, what is the c
- You are building a rectangular deck. The area of the deck should be 250 ft squared. You want the length of the deck to be 5 ft longer than twice its width. What should the dimensions of the deck be?
- A 3-foot-wide wood deck will be built around a rectangular-shaped pool that measures 15 feet by 30 feet. The resulting shape is also rectangular. If the lumber costs $10 per square yard, what is the cost of the wood for the deck?
- A 3-foot-wide wood deck will be built around a rectangular-shaped pool that measures 15 feet by 30 feet. The resulting shape is also rectangular. If the lumber costs $10 per square yard, what is the cost of the wood for the deck? a. $275 b. $306 c. $340 d
- A carton is such that the sum of its height h, length x, and width y equals 108 inches. The carton has a square base. We wish to maximize the volume of the box. To find the dimensions of the carton wi
- A large plywood box has a volume of 180 ft^3. Its length is 9 ft greater than its height, and its width is 4 ft less than its height. What are the dimensions of the box?
- A large plywood box has a volume of 96 ft^3. Its length is 8 ft greater than its height, and its width is 2 ft less than its height. What are the dimensions of the box?
- A large plywood box has a volume of 240 ft^3 . Its length is 16 ft greater than its height, and its width is 1 ft less than its height. What are the dimensions of the box?
- A rectangular countertop is 16 inches longer than it is wide. If the area of the countertop is 420 square inches, find the length and the width.
- A box with an open top is to be constructed out of a rectangular piece of cardboard with dimensions length=7 ft and width = 10 ft by cutting a square piece out of each corner and turning the sides up
- A box with an open top is to be constructed out of a rectangular piece of cardboard with dimensions length = 11 ft and width = 8 ft by cutting a square piece out of each corner and turning the sides up as shown in the picture.
- An open box is to be made from a rectangular piece of material by cutting equal squares from each corner and turning up the sides. Find the length, width, and height of the box of maximum volume if the material has dimensions of 12 feet by 8 feet.
- For a given box, the height measures 4 meters. If the length of the rectangular base is 2 meters greater than the width of the base and the lateral area L is 96 square meters, find the dimensions of the box.
- A 4 ft high and 6 ft width rectangular plate is submerged vertically in water so that the top is 2 ft below the surface. Express the hydrostatic force against one side of the plate as an integral and
- Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 1.4 times the width w of the rectangle. If the cross-sectional area is A, determi
- A rectangular storage building is 30 feet long and 25 feet wide. Find the ratio of the length to the perimeter of the building.
- A rectangular prismatic tank has the following dimensions: length is 3 m, width is 2 m. And depth is 3 m. It is being filled with water and the surface level is rising at 20 cm/min. What is the inflow
- The height of a rectangular box is 4 ft. The length is 1 ft longer than twice the width x. The volume is 312 ft cubed?
- I have a rectangular prism with a volume of 48 cubic feet and a height of 3/4 foot. The base of the rectangular prism is not a square and the width is greater than 2 feet. What is the length and width
- a) A long rectangular sheet of metal 12 in wide is to be made into a trough by turning up two sides to form right angles. Find the dimensions of the trough that give it maximum capacity. \\ b) A cyli
- A rectangular retaining wall has area 15 square feet. The height of the wall is two feet less than its length. Find the height and the length of the wall.
- A rectangular retaining wall has an area of 15 square feet. The height of the wall is two feet less than its length. Find the height and the length of the wall.
- A box (with no top) is to be constructed from a piece of cardboard of sides 8 and 5 by cutting out squares of length h from the corners and folding up the sides. Find the value of h that maximizes the
- A box (with no top) is to be constructed from a piece of cardboard of sides A and B by cutting out squares of length h from the corners and folding up the sides. Find the value of h that maximizes th
- A box (with no top) is to be constructed from a piece of cardboard of sides A and B by cutting out squares of length h from the corners and folding up the sides. Find the value of h that maximizes the
- A rectangular box with no top is to be made by cutting squares with side lengths of 5 inches from each corner of a square piece of cardboard. If the box must have a volume of 300 in^3, then what must the dimensions of the square piece of cardboard be? (Ro
- An open box is to be made out of an 8-inch-by-18-inch rectangular piece of cardboard by cutting out squares of equal size from the four corners and bending up the sides. Find the dimensions of the
- An open top rectangular box is constructed from a 100 ft.by 16 ft. Piece of cardboard by cutting squares of equal length from the corners and folding up the sides.Find the dimensions of the box that
- A rectangular field has an area of 2400 sq. m. is to be enclosed by a fence, and then divided into two lots by another fence set parallel to one of the sides (see Figure below). What must be the dimensions
- A rain gutter is formed by bending up the sides of a 30-inch-wide rectangular metal sheet. a) Find a function that models the cross-sectional area of the gutter in terms of height x. b) Find the value of x that maximizes the cross-sectional area of the gu
- You want to build a box with a square base. Let B be the length of one side of the base, and let H be the height, both measured in meters. Given the constraints that 10 is less than or equal to B and
- Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 0.3 times the width w of the rectangle (as shown in the figure below). If the cross-s
- An open box with a rectangular base is to be constructed from a square piece of metal which is 3 feet wide by cutting out a square from each of the four corners and bending up the sides. Find the maximum volume of such a box.
- A box with an open top is to be constructed out of a rectangular piece of cardboard with dimensions length=11ft and width=6ft by cutting a square piece out of each corner and turning the sides up as shown in the picture. Determine the length x of each
- A rectangular piece of cardboard that measures 4 inches by 3 inches is to be formed into a rectangular box by cutting squares with length x from each corner and folding up the sides. Find the volume o
- There is a rectangular box whose length x, width y and height z are changing at the following rates: the length x is decreasing at a rate of 2 ft/hour, the width y is increasing at a rate of 1 ft/hour
- 1) A long rectangular sheet of metal 12 in. wide is to be made into a trough by turning up two sides to form right angles. Find the dimensions of the trough that give it maximum capacity. 2) A cylind
- A rectangular solid (with a square base) has a surface area of 73.5 square centimeters. Find the dimensions that will result in a solid with maximum volume. Use that a rectangular solid with a height of h and square base with side length s has a surface a
- An open box is to be made from a 33 ft by 88 ft rectangular piece of sheet metal by cutting out squares of equal size from the four corners and bending up the sides. Find the maximum volume that the b
- An open box is to be made from a 21 ft by 56 ft rectangular piece of sheet metal by cutting out squares of equal size from the four corners and bending up the sides. Find the maximum volume that the b